Question

Triangle JKM with side j across from angle J, side k across from angle K, and side m across from angle M. If ∠J measures 45°, ∠M measures 40°, and j is 7 feet, then find m using the Law of Sines. Round your answer to the nearest tenth.

a) 9.2 feet
b) 10.5 feet
c) 12.3 feet
d) 8.6 feet

Answer 1

Using the Law of Sines in triangle JKM with ∠J = 45°, ∠M = 40°, and side j = 7 feet, we found that side m is approximately 12.3 feet. The Law of Sines relates the sides and angles of a triangle, allowing us to determine the length of side m based on the given information.

thus the correct option is (c)

Step-by-step explanation:

In the given triangle JKM, we know ∠J = 45°, ∠M = 40°, and side j = 7 feet. We can use the Law of Sines, which states that in any triangle, the ratio of the length of a side to the sine of its opposite angle is constant. Mathematically, this law is represented as

`\( (a)/(\sin A) = (b)/(\sin B) = (c)/(\sin C) \).`

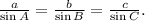
In our case, let's denote side k as
`\( k \)` and side m as
`\( m \)`. The law of sines for triangle JKM can be written as:

`\[ (j)/(\sin J) = (k)/(\sin K) = (m)/(\sin M) \]`

Substitute the given values:

`\[ (7)/(\sin 45°) = (k)/(\sin K) = (m)/(\sin 40°) \]`

Solving for
`\( m \)`:

`\[ m = (7 * \sin 40°)/(\sin 45°) \]`

Calculating this gives us
`\( m \approx 12.3 \)` feet.

Therefore, the length of side
`\( m \)` is approximately 12.3 feet when rounded to the nearest tenth.In summary, we applied the Law of Sines to relate the sides and angles of triangle JKM, and by solving the equation, we found that the length of side
`\( m \)` is approximately 12.3 feet. This method is a fundamental approach in trigonometry when dealing with non-right triangles, providing a useful tool for solving various geometric problems.

therefore correct option is (c)