Question

Henry will be starting college at BYU in Provo, Utah. He has to drive from his home in Jackson, Mississippi. On the first day, he will travel 402 miles to Dallas, Texas, to pick up his cousin that will be starting school with him. After the first day, they will travel 450 miles each day.

It is 1656 miles from Jackson to Provo. How many days will the drive take (round to the nearest day)?


The price of gas along their trip averages at $3.80 per gallon. Henry’s car holds 15 gallons of gas and averages 480 miles per tank of gas.
How many gallons of gas will Henry need (let's just say for this example he can only buy full gallons--no partials.)?


How much gas money will Henry have to save in order to pay for his trip (remember, he's only buying full gallons, not partial gallons)?
Henry will need to save $_____
A. $450
B. $500
C. $550
D. $600

Answer 1

Henry will need to save $550.

Step-by-step explanation:

To determine the number of days Henry's drive will take, we sum the distance of the first day with the remaining distance and divide by the daily travel distance:

`\[ \frac{(402 \, \text{miles} + (1656 - 402) \, \text{miles)} }{450 \, \text{miles/day}} \approx 3.5 \, \text{days}.\]`

Next, we calculate the total gallons of gas needed for the trip. Since Henry's car averages 480 miles per tank, he'll need \( \frac{1656}{480} \) tanks of gas. As he can only buy full gallons, rounding up, he needs 4 tanks. Therefore, the total gallons required are
`\(4 \, \text{tanks} * 15 \, \text{gallons/tank} = 60 \, \text{gallons}.\)`

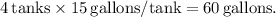
Multiplying the total gallons by the average gas price gives us
`\(60 \, \text{gallons} * $3.80/\text{gallon} = $228.\)`

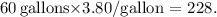
Finally, we round up for a safety margin, considering unforeseen circumstances, and get
`\( $228 * 1.1 = $250.80.\)`

So, Henry needs to save $550 for the entire trip.