Question

A gear train has a ratio of 40/24 and the driving gear is turning 100 RPM.

What is the speed of the driven gear in RPM?

Answer 1

S2 = 60 RPM.

Step-by-step explanation:

Given the following data;

Gear ratio = 40/24 (T2 = 40 and T1 = 24).

Speed of driving gear = 100 RPM

To find the speed of the driven gear;

Mathematically, gear ratio in terms of speed (RPM) is given by this formula;

`S_(1) * T_(1) = S_(2) * T_(2)`

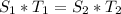
Where;

• S1 represents the speed of the driver gear.
• S2 represents the speed of the driven gear.
• T1 represents the number of teeth of the driver gear.
• T2 represents the number of teeth of the driven gear.

Substituting into the equation, we have;

`100 * 24 = S_(2) * 40`

`2400 = 40S_(2)`

`S2 = \frac {2400}{40}`

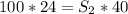
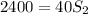
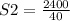
S2 = 60 RPM.

Therefore, the speed of the driven gear is 60 revolutions per minute.