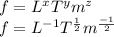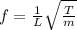Question

the frequency of a wave in a stretched string depends on the length L, tension T and linear density m with dimension ML-1 . deduce the formula for f in terms of L , T and M using dimensional analysis​

Answer 1

`f = (1 )/(L)\sqrt{(T)/(m) }`

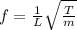
Step-by-step explanation:

Let the frequency ,

`f = L^(x)T^(y)m^(z)`

Now the unit of frequency is hertz = s⁻¹ = T⁻¹ where T is time, tension T = kgm/s² = MLT⁻¹ and linear density m = kg/m = ML⁻¹.

So,

`T^(-1) = L^(x)[MLT^(-2) ]^(y)[ML^(-1) ]^(z)\\`

collecting the like bases, we have

`T^(-1) = [L^(x + y -z)][M^(y + z) ][T^(-2y) ] \\L^(0) M^(0) T^(-1) = [L^(x + y -z)][M^(y + z) ][T^(-2y) ]`

Equating powers on both sides, we have

x + y - z = 0 (1)

y + z = 0 (2)

-2y = -1 (3)

From (3), y = 1/2

From (2), z = -y = -1/2

Substituting y and z into (1), we have

x + y - z = 0

x + 1/2 - (-1/2) = 0

x + 1/2 + 1/2 = 0

x + 1 = 0

x = -1

So,

`f = L^(x)T^(y)m^(z)\\f = L^(-1)T^{(1)/(2) }m^{(-1)/(2) }`

`f = (1 )/(L)\sqrt{(T)/(m) }`