Final answer:
i)

ii)
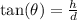
iii)

Step-by-step explanation:
To determine the height of the hill, we can utilize the tangent function in trigonometry, which relates the angle of elevation
 to the height (\(h\)) and horizontal distance
to the height (\(h\)) and horizontal distance
 The trigonometric ratio for this scenario is given by
The trigonometric ratio for this scenario is given by
 where
where
 represents the height of the hill and \(d\) is the horizontal distance from the surveyor to the base of the hill. Rearranging this formula gives us the equation h =
represents the height of the hill and \(d\) is the horizontal distance from the surveyor to the base of the hill. Rearranging this formula gives us the equation h =
 which allows us to find the height of the hill when given the angle and horizontal distance.
which allows us to find the height of the hill when given the angle and horizontal distance.
In this specific case, the horizontal distance
 is 100 meters, and the angle of elevation (\(\theta\)) is 17 degrees. By substituting these values into the formula
is 100 meters, and the angle of elevation (\(\theta\)) is 17 degrees. By substituting these values into the formula
 we can calculate the height of the hill. This computation results in the determination of the hill's height based on the surveyor's position and the angle at which the top of the hill is sighted.
we can calculate the height of the hill. This computation results in the determination of the hill's height based on the surveyor's position and the angle at which the top of the hill is sighted.
Trigonometric ratios provide a powerful tool for solving problems involving angles and distances in various contexts, allowing us to calculate unknown values such as heights, distances, or angles in a triangle when certain information is given. The tangent function, in particular, helps determine the height of the hill in this scenario, enabling accurate measurements without needing to physically access the top of the hill.
"Trigonometry, through the tangent function, relates the angle of elevation to the height and horizontal distance, allowing precise calculations of otherwise inaccessible heights, as demonstrated in this hill measurement scenario."