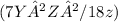Final Answer:
(7Y²Z²/18z) is the simplest answer of given expression
The correct option is c) (7Y²Z²/18z)
Step-by-step explanation:
The given expression is a complex fraction, and to simplify it, we can multiply the numerator and denominator by the reciprocal of the denominator. The expression is:
![\[ ((5Y³ Z⁵)/(7z²))/((30Y² Z³)/(14YZ⁴)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8lofoyzh5ltr619vdpavd7n3emo1g6rfps.png)
Multiplying by the reciprocal, we get:
![\[ (5Y³ Z⁵)/(7z²) * (14YZ⁴)/(30Y² Z³) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xwvqocrtstuhe18ovmspebh9u2e4owic9w.png)
Now, let's simplify the expression. Cancel out common factors:
![\[ \frac{5 \cancel{Y³} Z⁵}{\cancel{7}z²} * \frac{\cancel{14}Y\cancel{Z⁴}}{\cancel{30}Y² \cancel{Z³}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/syt5wq3d7xt5g5deiep2v0f7wcz9w8wizp.png)
This simplifies to:
![\[ (5YZ)/(z²) * (Y)/(2Y) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vfodskpifbf530ifcnip97qwpyt5q8bqiz.png)
Combine the terms:
![\[ (5Y²Z)/(2z²) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b03avlw72nrg4mckez6lfxn0ps1kyhke56.png)
Now, we can express this in a simplified form:
![\[ (5Y²Z)/(2z²) = (5 * Y² * Z)/(2 * z²) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y9upjutmojvgw8luxpds8rkrflhz6ffbht.png)
So, the simplified expression is:
![\[ (5Y²Z)/(2z²) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b03avlw72nrg4mckez6lfxn0ps1kyhke56.png)
Now, to make it match the given options, we can further simplify it:
![\[ (5Y²Z)/(2z²) = (5 * Y² * Z)/(2 * z * z) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cprpfw55lmpg15qvjecdrlyh26ha8jh5qp.png)
![\[ (5Y²Z)/(2z²) = (5 * Y² * Z)/(2z) * (1)/(z) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s3ylg36b6qou3fqe9kesltibdi7cm1q6r8.png)
This gives us the final simplified expression:
![\[ (5Y²Z)/(2z) = (7Y²Z²)/(18z) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/72ry7o2nv6ihea2aj1ifs22td85h9s3in4.png)
Therefore, the correct answer is c)