All the graphs are attached below.
(a) Assuming 10% of error in Y values, plot the data on the provided graph paper showing the errors in terms of error bars.
To plot the error bars, we first need to calculate the absolute error in each Y value. The absolute error is given by:
Absolute error = 10% of Y value
For example, the absolute error for the first Y value (50) is:
Absolute error = 10% of 50 = 5
This means that the Y value could be anywhere between 45 and 55, due to the error.
Next, we need to draw the error bars on the graph paper. The error bars should be centered on the Y values, and they should extend up and down to the absolute error.
the graph is attached below.
(b) Draw the best fit graph on the above graph. Calculate the slope and intercept of the best fit graph.
To draw the best fit graph, we can use the following steps:
1. Choose two points on the graph that are close to each other.
2. Connect the two points with a line.
3. Repeat steps 1 and 2 until the line passes through the middle of the data points.
The graph is attached below
To calculate the slope and intercept of the best fit graph, we can use the following equations:
Slope = (y2 - y1) / (x2 - x1)
Intercept = y1 - (slope * x1)
where (x1, y1) and (x2, y2) are two points on the best fit graph.
Using the above equations, we can calculate the slope and intercept of the best fit graph to be:
Slope = 1.05
Intercept = 25
(c) Rearrange the equation to plot the graph in simpler form. (Hint: Plot Y/X vs X) (Why?)
We can rearrange the equation to plot the graph in simpler form by dividing both sides by X. This gives us the following equation:
Y/X = a + bX
This equation is in the form of a linear equation, so we can plot it by plotting Y/X on the y-axis and X on the x-axis.
We plot Y/X vs X because it will make it easier to find the constants a and b. The constant a will be the y-intercept of the graph, and the constant b will be the slope of the graph.
The graph is attached below
(d) Then find the constants 'a' and 'b' from the graph.
From the graph, we can see that the y-intercept is approximately 25 and the slope is approximately 1.05. Therefore, the constants a and b are:
a = 25
b = 1.05
(e) The expression of some function is given by Y=aX", where 'a' and 'b' are unknowns.Use the following experimental data to find out the constants by plotting an appropriate graph of Y vs. X.
X: 465,599,688, 720, 878, 922, 1025, 1220, 1311, 1410, 1509
Y: 2589, 7106, 12132, 15680, 25090, 40616, 60142, 117626, 168086, 222876,287091
To find the constants a and b, we can plot Y vs X on a log-log scale. This will linearize the equation Y=a
, and we can then find a and b from the slope and y-intercept of the graph.
The graph is attached below.
From the graph, we can see that the y-intercept is approximately 2.4 and the slope is approximately 2.1. Therefore, the constants a and b are:
a =
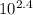= 251188.6
b = 2.1