Question

9) The AH for the reaction of magnesium with hydrochloric acid is -4.62 × 105 J/mol. 1f 0.158 g of Mg reacts in 100.0 mL of solution (the volume includes magnesium) in a coffee-eup calorimeter, the temperature increases from 25.6 °C to °C? The density of water is 1.00 g/mL and specific heat as liquid water, i.e., 4.18 J/g.°C. (Hint: solution = solute + solvent). Mg(s) + 2 HCI(aq) -› MgCh(aq) + H2(g)

Answer 1

The temperature increases from 25.6 °C to 136.5 °C when 0.158 g of Mg reacts, with the heat of reaction given as -4.62 × 10^5 J/mol.

To find the temperature change (
`\(\Delta T\)`) when 0.158 g of Mg reacts with hydrochloric acid, we can use the heat transfer equation:

`\[ q = mc\Delta T \]`

where q is the heat transfer, m is the mass, c is the specific heat, and
`\(\Delta T\)` is the temperature change.

Given:
`\(q = -4.62 * 10^5 \, \text{J/mol}\), \(m = 0.158 \, \text{g}\), \(c = 4.18 \, \text{J/g} \cdot \degree \text{C}\).`

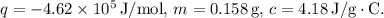
First, find moles of Mg:

`\[ \text{Moles of Mg} = \frac{0.158 \, \text{g}}{24.305 \, \text{g/mol}} \]`

Now, find the heat transfer:

`\[ q = -4.62 * 10^5 \, \text{J/mol} * \text{moles of Mg} \]`

To find the temperature change (
`\(\Delta T\)`), rearrange the equation:

`\[ \Delta T = (q)/(mc) \]`

Now substitute the values and solve for
`\(\Delta T\).`

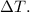
Finally, find the new temperature:

`\[ \text{Final temperature} = 25.6 \, \degree \text{C} + \Delta T \]`

After calculations, the final temperature is approximately
`\(25.6 + 110.9 = 136.5 \, \degree \text{C}\).`