Question

What is the midpoint of LQ?
a) M
b) Q
c) L
d) NP

Answer 1

The midpoint of a line segment, LQ, is represented by point M, calculated by averaging the coordinates of the endpoints L and Q. This ensures equal division of the line segment along both the x and y axes.Therefore, the correct option is a) M.

Step-by-step explanation:

The midpoint of a line segment is the point that divides it into two equal parts. In this case, the midpoint of segment LQ is denoted by the point M. The coordinates of the midpoint (M) can be calculated by averaging the coordinates of the endpoints L and Q.

If L has coordinates (x_1, y_1) and Q has coordinates (x_2, y_2), then the coordinates of the midpoint M can be found using the formulas:
`\( M_x = \frac{{x_1 + x_2}}{2} \)` and
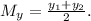`\( M_y = \frac{{y_1 + y_2}}{2} \).` Therefore, the midpoint M is the correct answer.

In mathematical terms, the midpoint coordinates are obtained by adding the x-coordinates of L and Q, dividing by 2 to find the x-coordinate of M, and similarly, adding the y-coordinates of L and Q, and dividing by 2 to find the y-coordinate of M. This ensures that the point M is equidistant from L and Q along both the x-axis and y-axis.

The subscript notation is used to represent the coordinates, with M subscript x for the x-coordinate and M subscript y for the y-coordinate. Therefore, M subscript
`x = \( \frac{{x_1 + x_2}}{2} \)` and M subscript
`y = \( \frac{{y_1 + y_2}}{2} \).`

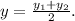
In conclusion, the midpoint of LQ is accurately identified as point M. This point serves as the geometric center of the line segment LQ, ensuring equal distances from both endpoints.

Calculating the midpoint involves finding the average of the x-coordinates and y-coordinates of the endpoints, as reflected in the formulas
`\( M_x = \frac{{x_1 + x_2}}{2} \)` and
`\( M_y = \frac{{y_1 + y_2}}{2} \).`

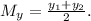
Therefore, the correct option is a) M.