Question

If the first and third terms of a geometric progression (G.P.) are √2 and 1/√2 , find the common ratio.

A. 1/2
B. 1/√2
C. 1/4
D. √2/2

Answer 1

In the given geometric progression with first term
`\( √(2) \)` and third term
`\( (1)/(√(2)) \)`, the common ratio is
`\( (1)/(√(2)) \)`, which corresponds to option B:
`\( (1)/(√(2)) \).`

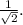
Step-by-step explanation:

In a geometric progression (G.P.), each term is found by multiplying the previous term by a constant factor called the common ratio (r).

Given the first term
`\(a_1 = √(2)\)` and the third term
`\(a_3 = (1)/(√(2))\)`, we can express the terms of the G.P. as:

`\[a_1 = √(2)\]`

`\[a_2 = a_1 \cdot r\]`

`\[a_3 = a_2 \cdot r = (√(2) \cdot r) \cdot r = (1)/(√(2))\]`

Now, we can set up an equation using these terms:

`\[√(2) \cdot r \cdot r = (1)/(√(2))\]`

To solve for (r), we can simplify the equation:

`\[2r^2 = (1)/(√(2))\]`

Now, multiply both sides by
`\(√(2)\)` to clear the fraction:

`\[2√(2) \cdot r^2 = 1\]`

`\[r^2 = (1)/(2√(2))\]`

Now, take the square root of both sides:

`\[r = \pm \frac{1}{\sqrt{4√(2)}}\]`

Simplify the denominator:

`\[r = \pm (1)/(√(8))\]\[r = \pm (1)/(2√(2))\]`

So, the correct common ratio is
`\( (1)/(√(2)) \)`, which corresponds to option B.