Given:
The graph of a polynomial.
To find:
The polynomial function for the given graph.
Solution:
If the graph of function intersect the x-axis at x=c, then (x-c) is a factor of that function f(x).
From the given graph it is clear that the graph of the polynomial function intersect the x-axis at x=-1, x=2, x=3.
So, (x+1), (x-2) and (x-3) are the factors of required polynomial.
At x=2 and x=3, it look like a linear function. So, the multiplicity of (x-2) and (x-3) are 1.
At x=-1, it look like a cubic function. So, the multiplicity of (x+1) is 3.
The required polynomial is
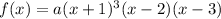 ...(i)
...(i)
The function passes through the point (1,10). Putting x=1 and f(x)=10, we get
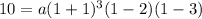
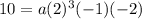
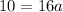
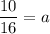
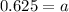
Putting a=0.625 in (i), we get

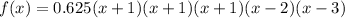
Therefore, the required polynomial function is
 or it can be written as
or it can be written as
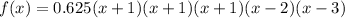 .
.