Answer:
1.

2. 9.8 m
3. 8.7 m.
Explanation:
1. Let the angle be represented by θ, so that:
Cos θ =

=
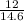
Cos θ = 0.82192
θ =
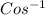 0.8219
0.8219
=
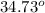
θ =

The angle through which the boy must raise his eyes to see the top of the cross on the tower is
 .
.
2. Let the height from the boy's head to the top of the cross be represented by y, so that:
Sin
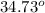 =
=
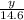
y = Sin
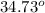 x 14.6
x 14.6
= 0.5697 x 14.6
y = 8.32 m
The height of the top of the cross from the ground = 1.5 + 8.32
= 9.82 m
The height of the top of the cross from the ground is 9.8 m.
3. Let the height from the boy's head to the top of the building be represented by x, so that:
Tan 31 =
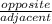
=
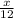
x = Tan 31 x 12
= 0.6009 x 12
x = 7.21
The height of the church building = 1.5 + 7.21
= 8.71
The height of the church building is 8.7 m.
The sketch to the question is attached to this answer.