Question

The schematic diagram below shows three machines in a production unit connected to a 240 volt supply.

The layout uses different types of wire for the main wire, wire 1, wire 2, and wire 3.
Calculate the maximum current that can flow through each type of wire. The diameter of a wire is related to the maximum amount of current it
can safely carry. Use Internet resources to find the most suitable gauge of wire for each part of the wiring in the circuit. List the highest American
Wire Gauge (AWG) number that you can use for each type of wire. (Hint: For the main wire, consider how the current through it relates to the
currents through each of the machines.)
Also, state how you can protect the wiring from damage If any of the machines exceeds its maximum power rating because of a malfunction.

Answer 1

`\begin{array}{ccc}Wire \ Number &Maximum\ \ Current \ (A)& AWG\\&&\\Main \ Wire&16(5)/(6) &9\\&&\\Wire \ 1&9(1)/(6) &12\\&&\\Wire \ 2&5&14\\&&\\Wire \ 3&2.5&17\end{array}`

Step-by-step explanation:

The given parameters of the circuit are;

The voltage applied to the circuit = 240 volt

The types of wire in the circuit are Main wire, wire 1, wire 2, and wire 3

The maximum current that can flow through each type of wire is given by the max power of the machine powered by the wire

Power, P = Voltage, V × Current, I

∴ I = P/V

The maximum power of the machine powered by wire 1 = 2,200 W

The current flowing through wire 1, I₁ = 2,200 W/(240 V) = 55/6 A =
`9(1)/(6) \, A`

The maximum power of the machine powered by wire 2 = 1,200 W

The current flowing through wire 2, I₂ = 1,200 W/(240 V) = 5 A

The maximum power of the machine powered by wire 3 = 600 W

The current flowing through wire 3, I₃ = 600 W/(240 V) = 2.5 A

Therefore, Kirchhoff's current law, we have;

The current that the main wire can carry, I = I₁ + I₂ + I₃

∴ I = 55/6 A + 5 A + 2.5 A = 50/3 A = 16.
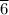`\overline 6` A

The current that the main wire can carry, I = 16.
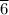`\overline 6` A

The highest American Wire Gauge (AWG) that can be used for each type of wire are listed as follows;

`\begin{array}{ccc}Wire \ Number &Maximum\ \ Current \ (A)& AWG\\&&\\I&16(5)/(6) &9\\&&\\I_1&9(1)/(6) &12\\&&\\I_2&5&14\\&&\\I_3&2.5&17\end{array}`

Therefore, we have;

`\begin{array}{ccc}Wire \ Number &Maximum\ \ Current \ (A)& AWG\\&&\\Main \ Wire&16(5)/(6) &9\\&&\\Wire \ 1&9(1)/(6) &12\\&&\\Wire \ 2&5&14\\&&\\Wire \ 3&2.5&17\end{array}`