Question

1 kg of fertilizer cover and area of half square metre find the amount of fertilizer acquired by farmer for a circular field whose radius is 14m

​

Answer 1

The circular field would require 1232 kg of fertilizer.

Explanation:

0.5
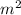`m^(2)` takes 1 kg of fertilizer.

For a circular field of radius 14 m, its area = area of a circle

area of a circle =
`\pi`
`r^(2)`

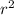
So that,

Area of the circular field =
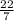`(22)/(7)` x 14 x 14

= 22 x 2 x 14

= 616

Area of the field = 616
`m^(2)`

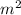
Since, 0.5
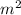`m^(2)` takes 1 kg of fertilizer. Let the kilograms of fertilizer required by the field be represented by x.

Thus,

x =
`(616*1)/(0.5)`

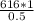
= 1232

x = 1232 kg

Therefore, the circular field would require 1232 kg of fertilizer.