Question

Draw a lift pump diagram and explain how it operates.

Solve the following problems
A metal box of weigh 20 N rests on its 1 m by 0.6m side on floor. How
much is the pressure exerted by the metal box on the floor? Take ga
10 m/s?
A rectangular container of base 50 cm by 30 cm is filled with water to a
depth of 5 cm. How much is the pressure exerted at the base?
(Take pw= 1000 kg/m3 and g =10 m/s2)
How much is the pressure exerted at a point where a ball- pointed
pen of area 1mm? is pushed against the paper with a force of 24 N?
Suppose a scientist was able to construct a barometer with a liquid
being twice denser than mercury, then how high would the liquid raise
ard pressure?
m. if the
oil to a​

Answer 1

1) The pressure exerted by the metal box on the floor is 33.
`\overline 3` Pa

2) The pressure exerted at the base is 250 Pa

3) The pressure exerted at the point where the pen pushes against the paper is 24 MPa

Step-by-step explanation:

1) Pressure is given by the following relation

`Pressure, P = (Force, F)/(Area, A)`

`\therefore P = (F)/(A)`

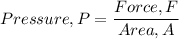
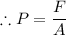
The force exerted by the weight of the metal box, F = 20 N

The dimensions of the side on which the metal box rests = 1 m by 0.6 m

∴ The area of the side on which the metal box rests, A = 1 m × 0.6 m = 0.6 m²

The pressure exerted by the metal box on the floor, 'P' is therefore given as follows;

`\therefore P = (F)/(A) = (20 \, N)/(0.6 \, m^2) = (100)/(3) \ Pa = 33.\overline 3 \ Pa`

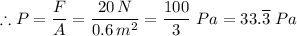
The pressure exerted by the metal box on the floor, P = 33.
`\overline 3` Pa

2) The dimensions of the rectangular container are;

Base dimension = 50 cm by 30 cm = 0.5 m by 0.3 m

The depth to which the water is filled in the container = 5 cm = 0.05 m

The density of water,
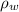`\rho_w` = 1,000 kg/m³

The volume of water in the container, V = Base area × Height = 0.5 m × 0.3 m × 0.05 m = 0.0075 m³

∴ V = 0.0075 m³

The mass of the water, m = V ×
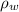`\rho_w` = 0.0075 m³ × 1,000 kg/m³ = 7.5 kg

m = 7.5 kg

The weight of the water, W = m × g = 7.5 kg × 10 m/s² = 75 N

The base area, A = 0.5 m × 0.6 m = 0.3 m²

The pressure exerted at the base, P = W/A = 75 N/(0.3 m²) = 250 Pa

The pressure exerted at the base, P = 250 Pa

3) The area of the point of the ball-pointed pen pushing against the paper, A = 1 mm² = 0.000001 m²

The force with which the point on the pen pushes against the paper = 24 N

The pressure exerted at the point where the pen pushes against the paper, P = W/A

∴ P = 24 N/(0.000001 m²) = 24,000,000 Pa

The pressure exerted at the point where the pen pushes against the paper, P = 24,000,000 Pa = 24 MPa.