Question

Solve for x 10x 44 and 8x-23

Answer 1

In the triangle, the midsegment 8x - 23 is parallel to 10x + 44. Solving for x, we find x = 15. This ensures the midsegment is half the length of the parallel side.

In a triangle with a midsegment, the midsegment is parallel to one side of the triangle, and its length is equal to half the length of that side.

Given the midsegment 8x - 23 is parallel to 10x + 44, we can set up the equation:
`8x - 23 = (1)/(2)(10x + 44)`

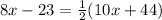
Now, solve for x:
`8x - 23 = 5x + 22`

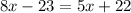
Subtract 5x from both sides: 3x - 23 = 22

Add 23 to both sides: 3x = 45

Divide by 3: x = 15

So, x = 15 is the solution.

The complete question is:

(attached)