Final Answer:
The average of two irrational numbers,
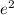 and √54, given by
and √54, given by
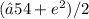 , is irrational, supporting the density of irrational numbers between them. Thus the option c is correct c.
, is irrational, supporting the density of irrational numbers between them. Thus the option c is correct c.
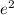 and √54
and √54
Step-by-step explanation:
To find an irrational number between
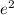 and √54, we can consider the average of these two values. Let's denote this average as x. Thus, x = (
and √54, we can consider the average of these two values. Let's denote this average as x. Thus, x = (
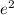 + √54)/2. Now, we need to show that x is irrational.
+ √54)/2. Now, we need to show that x is irrational.
Assume, for the sake of contradiction, that x is rational. This implies that both
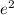 and √54 are also rational, as the sum and division of rational numbers result in rational numbers. However, we know that
and √54 are also rational, as the sum and division of rational numbers result in rational numbers. However, we know that
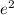 is irrational, and √54 is also irrational (since 54 is not a perfect square). This contradicts our assumption that x is rational, proving that x must be irrational.
is irrational, and √54 is also irrational (since 54 is not a perfect square). This contradicts our assumption that x is rational, proving that x must be irrational.
In summary, the irrational number (√54 +
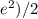 lies between
lies between
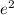 and √54, supporting the idea that irrational numbers are dense in real numbers.
and √54, supporting the idea that irrational numbers are dense in real numbers.