Question

A tree is 16 feet tall. A wire runs from the top of the tree to a point 6 feet from its base. The wire is √292 feet long. Estimate the length of the wire to the nearest hundredth of a foot.

(a) 26.91 feet
(b) 18.38 feet
(c) 21.50 feet
(d) 24.70 feet

Answer 1

The estimated length of the wire, rounded to the nearest hundredth of a foot, is approximately 24.70 feet, corresponding to option (d). Thus the correct option is d.

Step-by-step explanation:

To estimate the length of the wire, we can use the Pythagorean Theorem since the situation forms a right-angled triangle. Let h represent the height of the tree, b denote the distance from the base to the point where the wire touches the ground, and w represent the length of the wire. The Pythagorean Theorem is given by the formula
`\( w = √(h^2 + b^2) \).`

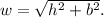
In this scenario, the tree is 16 feet tall, and the wire runs to a point 6 feet from its base. Applying the Pythagorean Theorem, we have
`w = √(16^2 + 6^2) = √(256 + 36) = √(292) \)` feet. Rounding this value to the nearest hundredth, we get approximately 24.70 feet, which corresponds to option (d).

Therefore, the estimated length of the wire to the nearest hundredth of a foot is 24.70 feet, making option (d) the correct choice based on the given alternatives.