Given:
A figure of a right angle triangle.
To find:
The length of the shorter leg.
Solution:
In a right angle triangle,
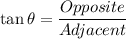
In the given triangle,
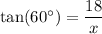
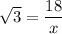
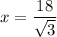
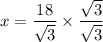
On further simplification, we get
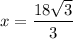
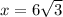
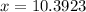
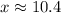
Therefore, the length of the shortest leg is 10.4 and the correct option is B.