Question

Q1) A pipe of radius 0.6 cm discharges petrol at a rate of 2.45 m/s. Find the volume of petrol discharged in 3 minutes, giving your answer in litres.

Q2) A pipe diameter 0.036 m discharges water at a rate of 1.1 m?s into a cylindrical tank with a base radius of 3.4 m and height of 1.4 m. Find the time required to fill the tank giving your answer correct to the nearest minute.

Answer 1

Q1) The volume of petrol discharged in 3 minutes is approximately 49.88 litres

Q2) The time it takes to fill the tank is approximately 12 hours 37 minutes

Explanation:

Q1) The flow rate of fluid from a pipe, 'Q' is given according to the following equation;

`Q = (V)/(t) =(A \cdot l)/(t) = A \cdot \overline v`

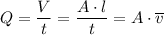
Where;

Q = The flow rate of fluid in the pipe

V = The volume that flows from the pipe in the given time

A = The cross sectional area of the pipe

t = The time it takes a given volume of fluid to flow from the pipe

l = The length of the pipe that the volume that flows in the given time takes in the pipe

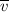`\overline v` = The rate at which the fluid flows

For a circular pipe, A = π·r²

r = The radius of the pipe

The given parameters in the question are;

r = 0.6 cm = 0.006 m

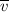`\overline v` = 2.45 m/s

Therefore, by plugging in the values, we get;

A = π·r² = π × (0.006 m)²

Q = A·
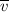`\overline v` = (π × (0.006 m²)) × 2.45 m/s

Q = (π × (0.006 m²)) × 2.45 m/s

V = Q × t

Where;

t = Time of flow = 3 minutes = 3 minutes × 60 seconds/minute = 180 seconds

t = 180 s

∴ V = Q × t = ((π × (0.006 m²)) × 2.45 m/s) × 180 s = 0.04987592496 m³

V = 0.04987592496 m³

1 m³ = 1,000 l

∴ 0.04987592496 m³ = 0.04987592496 m³ × 1,000 l/m³= 49.87592496 l

∴ V = 0.04987592496 m³ = 49.87592496 l ≈ 49.88 litres

The volume of petrol discharged in 3 minutes, V ≈ 49.88 litres

Q2) The given diameter of the pipe, d = 0.036 m

The rate at which water discharges into the cylindrical tank,
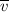`\overline v` = 1.1 m/s

The base radius of the cylindrical tank, R = 3.4 m

The height of the cylindrical tank, h = 1.4 m

Therefore, we have;

The radius of the pipe, r = d/2 = 0.036 m/2 = 0.018 m

The cross sectional area of the pipe, A = π·r² = π×( 0.018 m)²

The volume of the cylindrical tank, V = (The base area of the tank) × (The height of the tank)

∴ V = π × R² × h = π × (3.4 m)² × 1.4 m = π·16.184 m³

The flow rate of Q = A ×
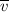`\overline v` = (π×( 0.018 m)²) × 1.1 m/s = π·0.0003564 m³/s

Q = V/t

∴ t = V/Q

Where;

t = The time it takes to fill a volume, 'V', at a flow rate 'Q'

∴ t = V/Q = (π·16.184 m³)/(π·0.0003564 m³/s) = 45409.6520763 s

t = 45409.6520763 s = 12 hours 36 minutes 49 seconds (using an online time converter)

Therefore, The time it takes to fill the tank, t ≈ 12 hours 37 minutes, after rounding to the nearest minute.