Question

William is staying in a cottage along a beautiful and straight shoreline. A point Q on the shoreline is located 3 kilometers east of the cottage, and an island is located 2 kilometers north of Q (see image below). William plans to travel from the cottage to the island by some combination of walking and swimming. He can start to swim at any point P between the cottage and the point Q. If he walks at a rate of 7 km/hr and swims at a rate of 5 km/hr, what is the minimum possible time it will take William to reach the island? Enter an exact answer or round to the nearest hundredth of an hour.

Answer 1

The minimum possible time is
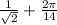`(1)/(√(2))} + (2\pi)/(14)` hours.

To minimize the time William takes to reach the island, he should swim at an angle that minimizes the total distance traveled. This angle can be found by considering the cottage, the point Q, and the island as vertices of a right-angled triangle.

Let the point where William starts swimming be P. The distance from the cottage to Q is 3 kilometers (east), and the distance from Q to the island is 2 kilometers (north). William will swim a distance x kilometers to reach the island.

The total distance traveled is the sum of the walking distance and swimming distance. The walking distance is 3−x, and the swimming distance is
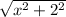`√(x^2+2^2)` (using the Pythagorean theorem). The total time T is given by the formula:

T= 3−x/7+
`√(x^2+2^2)/5`

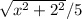
To find the minimum time, take the derivative of T with respect to x and set it equal to zero:

dT/dx=0

Solving this equation will give the value of x that minimizes the time. The solution is x=
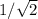`1/√(2)`. Substituting this value back into the original equation for T gives the minimum time:

T=
`(1)/(√(2))} + (2\pi)/(14)`

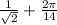
This represents the minimum time for William to reach the island by a combination of walking and swimming.