The area of the shaded segment of the circle with a 90-degree angle and a radius of 8 cm is 16π cm² or approximately
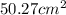
To find the area of the shaded segment of a circle, you need to know the radius of the circle and the angle of the segment. In this case, we are given that the angle is 90 degrees and the radius is 8 cm.
To calculate the area of the shaded segment, you can follow these steps:
1. Find the area of the entire circle by using the formula A = πr², where A is the area and r is the radius. In this case, the radius is 8 cm, so the area of the entire circle is A = π(8 cm)².
2. Since the shaded segment forms a 90-degree angle, it is one-fourth of the entire circle. To find the area of the shaded segment, divide the area of the entire circle by 4.
3. Substitute the values into the formula and calculate the area of the shaded segment.
For example, let's calculate the area of the shaded segment:
1. Area of the entire circle = π(8 cm)² = 64π cm².
2. Area of the shaded segment = (1/4) × 64π cm² = 16π cm².
Therefore, the area of the shaded segment of the circle with a 90-degree angle and a radius of 8 cm is 16π cm² or 50.27

The probable diagram could be