Question

Which is the graph of the given function?
f(1) = 3 cos(-t)

Answer 1

The graph of the given function
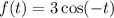`\(f(t) = 3 \cos(-t)\)` is a cosine function that is horizontally reflected about the y-axis and has an amplitude of 3.

Step-by-step explanation:

The function
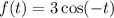`\(f(t) = 3 \cos(-t)\)` represents a cosine function with an amplitude of 3. The negative sign inside the cosine function indicates a horizontal reflection about the y-axis. The standard form of a cosine function is
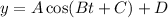`\(y = A \cos(Bt + C) + D\)`, where A is the amplitude, B is the frequency, C is the phase shift, and D is the vertical shift. In this case, A = 3, and the negative sign implies a reflection.

The amplitude of 3 signifies the maximum displacement of the cosine wave from its average value. Since the amplitude is positive, the graph oscillates between 3 and -3. The negative sign in front of \(t\) reflects the graph about the y-axis, causing a horizontal flip. Therefore, the final graph is a cosine curve with an amplitude of 3, horizontally reflected about the y-axis.

In summary, the function
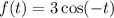`\(f(t) = 3 \cos(-t)\)` corresponds to a cosine graph with an amplitude of 3 and a horizontal reflection. Understanding the role of each component in the function helps visualize and interpret the characteristics of the graph accurately.