Question

Please I’m desperate and tell me how you did it

Answer 1

Given:

Triangle EFG is similar to triangle HIJ.

To find:

The measure of side IJ.

Solution:

We know that, corresponding sides of similar triangles are proportional.

Triangle EFG is similar to triangle HIJ.

`(EF)/(HI)=(FG)/(IJ)`

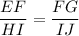
Putting the given values, we get

`(7)/(32)=(4)/(IJ)`

`7* IJ=4* 32`

`IJ=(128)/(7)`

`IJ=18.2857`

`IJ\approx =18.3`

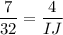
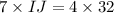
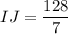
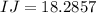
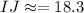
Therefore, the measure of side IJ is 18.3 units.