Question :
Choose SSS, SAS, or AA to prove the triangles are similar.
A. SSS
B. SAS
C. AA
Answer :
As, all sides are given so we can use SSS to prove the triangles are similar.
So, correct option is A.
Step-by-step explanation :
Given :
- Sides of 1st triangle = 24, 32 and 40
- Sides of 2nd triangle = 27, 36 and 45
To Prove :
Proof :
As, all three sides are given so let's check ratio of all three sides.
1.
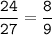
2.

3.
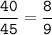
As, all sides are in equal ratio.
So, by SSS
∆1 ~ ∆2