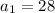Question

In an Arithmetic Progression, if d = -4, n = 7, an = 4, then find a1

Answer 1

`a_1 = 28`

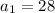
Explanation:

Arithmetic progression:

The nth term of an arithmetic progression is given by the following equation:

`a_n = a_1 + (n-1)d`

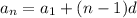
In which
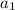`a_1` is the first term and d is the common difference between consecutive terms.

In this question, we have that:

`a_7 = 4, d = -4`

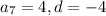
We want to find
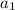`a_1`. So

`a_n = a_1 + (n-1)d`

`4 = a_1 + (7-1)(-4)`

`a_1 = 4 + 24 = 28`

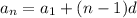
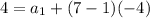
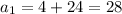
We have that
`a_1 = 28`