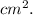Question

HELP ME WITH THIS PLEASE

Answer 1

The two solids represented by the nets are a rectangular prism with a surface area of 727.5
`cm^2` and a triangular prism with a surface area of 753.75
`cm^2.`

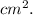
To make a model of the solid that is represented by each net, we can cut out the net along the solid lines and fold it along the dotted lines.

Net 1:

This net represents a rectangular prism. To make a model of the prism, we can cut out the net and fold it along the dotted lines. The two large rectangles will be the top and bottom faces of the prism, and the four smaller rectangles will be the sides. We can then tape or glue the edges of the net together to form the prism.

Net 2:

This net represents a triangular prism. To make a model of the prism, we can cut out the net and fold it along the dotted lines. The large triangle will be the base of the prism, and the three smaller triangles will be the sides. We can then tape or glue the edges of the net together to form the prism.

Once we have made the models of the solids, we can identify them and find their surface areas.

Solid 1:

The solid represented by Net 1 is a rectangular prism. The surface area of a rectangular prism is calculated as follows:

Surface area = 2(lw + wh + lh)

where l, w, and h are the length, width, and height of the prism.

From the net, we can see that the dimensions of the prism are 9.5 cm x 4.5 cm x 15 cm. Therefore, the surface area of the prism is:

Surface area = 2((9.5 cm)(4.5 cm) + (4.5 cm)(15 cm) + (9.5 cm)(15 cm))

Surface area = 727.5
`cm^2`

Solid 2:

The solid represented by Net 2 is a triangular prism. The surface area of a triangular prism is calculated as follows:

Surface area = 2B + Ph

where B is the area of the base triangle, P is the perimeter of the base triangle, and h is the height of the prism.

From the net, we can see that the dimensions of the base triangle are 15 cm x 6.5 cm x 9.5 cm. Therefore, the area of the base triangle is:

Area of base triangle = (1/2)(15 cm)(6.5 cm)

Area of base triangle = 48.75
`cm^2`

The perimeter of the base triangle is:

Perimeter of base triangle = 15 cm + 6.5 cm + 9.5 cm

Perimeter of base triangle = 31 cm

The height of the prism is 15 cm. Therefore, the surface area of the prism is:

Surface area = 2(48.75
`cm^2`) + (31 cm)(15 cm)

Surface area = 753.75
`cm^2`

Therefore, the two solids represented by the nets are a rectangular prism with a surface area of 727.5
`cm^2` and a triangular prism with a surface area of 753.75
`cm^2.`