Question

Determine whether the graphs of each pair of equations are parallel, perpendicular, or neither

Answer 1

Pairs
`\(y = 3x + 4\)` and
`\(y = 3x + 7\)` are parallel. Pairs
`\(y = -4x + 1\)` and
`\(4y = x + 3\)` are perpendicular. Pairs
`\(y = 2x - 5\)` and
`\(y = 4x - 5\)` are parallel. Pairs
`\(y = 7x + 2\)` and
`\(x + 7y = 8\)` are perpendicular. Pairs y = 6 and 3y = 9 are parallel. Pairs
`\(x + y = 4\)` and
`\(y = x - 3\)` are perpendicular.

Let's analyze each pair of equations to determine whether their graphs are parallel, perpendicular, or neither.

1.
`\(y = 3x + 4\)` and
`\(y = 3x + 7\)`:

Both equations have the same slope (3), so the graphs are parallel.

2.
`\(y = -4x + 1\)` and
`\(4y = x + 3\)`:

The first equation has a slope of -4, and the second equation can be rewritten as
`\(y = (1)/(4)x + (3)/(4)\)` (dividing both sides by 4).

The slopes are negative reciprocals
`(\(-4 * (1)/(4) = -1\))`, so the graphs are perpendicular.

3.
`\(y = 2x - 5\)` and
`\(y = 4x - 5\)`:

Both equations have the same slope (2), so the graphs are parallel.

4.
`\(y = 7x + 2\)` and
`\(x + 7y = 8\)`:

Rewrite the second equation in slope-intercept form:
`\(7y = -x + 8\) \(\Rightarrow\) \(y = -(1)/(7)x + (8)/(7)\).`

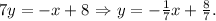
The slopes are negative reciprocals
`(\(7 * -(1)/(7) = -1\))`, so the graphs are perpendicular.

5. y = 6 and 3y = 9:

Divide the second equation by 3 to get y = 3.

Both equations have the same constant slope, so the graphs are parallel lines.

6.
`\(x + y = 4\)` and
`\(y = x - 3\)`:

Rewrite the first equation to slope-intercept form:
`\(y = -x + 4\)`.

The slopes are negative reciprocals
`(\(-1 * 1 = -1\)`), so the graphs are perpendicular.

The probable question may be:

"Determine whether the graphs of each pair of equations are parallel, perpendicular, or neither

y= 3x + 4;y= 3x + 7

y=-4x + 1: 4y = x + 3

y=2x-5;y= 4x-5

y= 7x + 2; x + 7y=8

y=6; 3y=9

x + y = 4;y=x - 3"