Question

Two metal rods in a factory are oppositely charged and placed 8.9 cm apart. One rod has a charge of +7.5×10−7 C and the other has a charge of −5.1×10−5 C. What is the force between the rods?

Answer 1

The force between the oppositely charged metal rods is -2.987 N, indicating an attractive force.

Step-by-step explanation:

The force between two oppositely charged metal rods can be calculated using Coulomb's law. Coulomb's law states that the force between two charges is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance between them.

To calculate the force, we can use the equation:

`F = k * (q1*q2) / r^2`

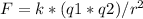
, k is the electrostatic constant

`(9 * 10^9 Nm^2/C^2),`

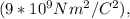
q1 and q2 are the magnitudes of the charges, and r is the distance between the charges.

Plugging in the values from the question, we get:

`F = (9 * 10^9 Nm^2/C^2) * ((7.5 * 10^-7 C) * (-5.1 * 10^-5 C)) / (0.089 m)^2`

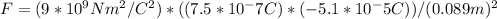
= -2.987 N.

The force between the rods is -2.987 N, which means it is attractive. The negative value indicates that the force is attractive, while a positive value would indicate a repulsive force.

Answer 2

43.4 N

Step-by-step explanation:

The force between two point charges can be calculated using Coulomb's Law, which is given by:

`F=(k\big|q_1q_2\big|)/(r^2)`

Where:

• 'F' is the force between the charges
• 'k' is Coulomb's constant (8.99 × 10⁹ Nm²/C²)
• 'q₁' and 'q₂' are the magnitudes of the charges
• 'r' is the distance between the charges in meters

We are given:

• q₁ = 7.5 × 10⁻⁷ C
• q₂ = −5.1 × 10⁻⁵ C
• r = 8.9 cm = 0.089 m

Plug in our values and solve:

`\Longrightarrow F=\frac{(8.99 * 10^(9) \text{ $\frac{\text{Nm$^2$}}{\text{C$^2$}}$})(7.5 * 10^(-7) \text{ C})(5.1 * 10^(-5) \text{ C})}{(0.089 \text{ m})^2}\\\\\\\\\therefore F = \boxed{43.4 \text{ N}}`

The force between the two metal rods, given their charges and the distance apart, is approximately 43.4 Newtons. ​