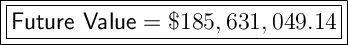Question

An investment of $85,500.00 earns 19.7% annual interest, compounded continuously. If no funds are added or removed from this account, what is the future value of the investment after 39 years? Round your answer to the nearest penny.

Answer 1

$185,631,049.14

Explanation:

To calculate the future value of an investment of $85,500 after 39 years that earns 19.7% annual interest compounded continuously, we can use the Continuous Compounding Interest formula:

`\boxed{\begin{array}{l}\underline{\textsf{Continuous Compounding Interest Formula}}\\\\A=Pe^(rt)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\;\textsf{$A$ is the final amount.}\\\phantom{ww}\bullet\;\;\textsf{$P$ is the principal amount.}\\\phantom{ww}\bullet\;\;\textsf{$e$ is Euler's number (constant).}\\\phantom{ww}\bullet\;\;\textsf{$r$ is the interest rate (in decimal form).}\\\phantom{ww}\bullet\;\;\textsf{$t$ is the time (in years).}\end{array}}`

In this case:

• P = $85,500
• r = 19.7% = 0.197
• t = 39 years

Substitute the values into the formula and solve for A:

`A=85500\cdot e^(0.197 \cdot 39)`

`A=85500\cdot e^(7.683)`

`A=85500\cdot 2171.1233817...`

`A=185\:631\:049.13535...`

`A=\$185,631,049.14`

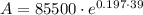
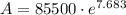
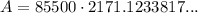
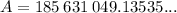
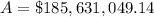
Therefore, the future value of the investment after 39 years is:

`\Large\boxed{\boxed{\textsf{Future Value}=\$185,631,049.14}}`