Given polynomial to us is
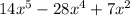
According to the question we need to factor it in the form of
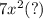 , and we need to find the value of "?" .
, and we need to find the value of "?" .
For that divide the whole polynomial by
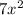 . We would get ,
. We would get ,
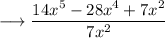
we can write it as,
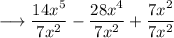
simplify,

Hence the final factored form will be,
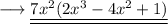
and we are done!