Question

Factor the polynomial.
14x^⁵-28x^4+7x^2
7x^2(????????)
Please help someone

Answer 1

Given polynomial to us is
`14x^5-28x^4+7x^2`

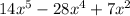
According to the question we need to factor it in the form of
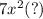`7x^2(?)` , and we need to find the value of "?" .

For that divide the whole polynomial by
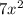`7x^2` . We would get ,

`\longrightarrow (14x^5-28x^4+7x^2)/(7x^2)\\`

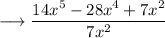
we can write it as,

`\longrightarrow (14x^5)/(7x^2)-(28x^4)/(7x^2)+(7x^2)/(7x^2)\\`

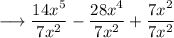
simplify,

`\longrightarrow 2x^3-4x^2+1`

Hence the final factored form will be,

`\longrightarrow \underline{\underline{ 7x^2(2x^3-4x^2+1)}}`

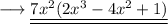
and we are done!

Answer 2

`7x^2(2x^3-4x^2+1)`

Explanation:

Given polynomial:

`14x^5-28x^4+7x^2`

Rewrite the numbers as multiples of 7:

`\implies 7 \cdot 2x^5-7 \cdot 4x^4+7 \cdot 1x^2`

Factor out the common term 7:

`\implies 7(2x^5-4x^4+x^2)`

Rewrite the exponents as sums:

`\implies 7(2x^(2+3)-4x^(2+2)+x^(2+0))`

`\textsf{Apply exponent rule} \quad a^(b+c)=a^b \cdot a^c`

`\implies 7(2x^(2)x^3-4x^(2)x^2+x^(2)x^0)`

`\implies 7(2x^(2)x^3-4x^(2)x^2+1x^(2))`

Factor out the common term x²:

`\implies 7x^2(2x^3-4x^2+1)`