Question

A spring constant k=8.75 N/m is hung vertically from a rigid support. A mass of 0.500kg is placed on the end of the spring and supported by hand at a point so that the displacement of the spring is 0.250 m. The mass is suddenly released and allowed to fall. At the lowest position of the mass what is the displacement of the spring from its equilibrium position? (hint--Apply equation 5 (mg(x2-x1)=1/2k(x2^2-x1^2) with x1= 0.250m and x the unknown. this will lead to a quadratic eq.)

Answer 1

The displacement of the spring from its equilibrium position at the lowest position of the mass is approximately 1.80952 m.

Step-by-step explanation:

According to equation 5,
`mg(x_2-x_1) = 1/2k(x_2^2-x_1^2)`.

Plugging in the given values: m = 0.500 kg, x₁ = 0.250 m, and k = 8.75 N/m, we can solve for x₂.

Rearranging the equation, we get:

`0.500 kg * 9.8 m/s^2 * (x_2 - 0.250 m) = 1/2 * 8.75 N/m * (x_2^2 - (0.250 m)^2)`

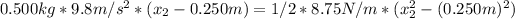
Simplifying the equation gives:

4.9x₂ - 1.225 = 4.375x₂ - 0.2734375

0.525x₂ = 0.9515625

x₂ = 1.80952 m

Therefore, the displacement of the spring from its equilibrium position at the lowest position of the mass is approximately 1.80952 m.