Question

Eli is making a model castle out of clay. One of the roof peaks is in the shape of a cone with a diameter of 14 inches and a slant height of 20 inches. What is the surface area of the cone peak? Round your answer to the nearest hundredth. Use 3.14 for pi. (1 point) square inches​

Answer 1

The surface area of the cone peak in Eli's model castle is 439.60 square inches, found by using the formula A = πrl, with a radius of 7 inches and a slant height of 20 inches.

Step-by-step explanation:

To calculate the surface area of Eli's model castle cone peak, we need to consider the formula for the lateral surface area of a cone, which is A = πrl, where r is the radius and l is the slant height. Since the cone's diameter is 14 inches, the radius would be half of that, which is 7 inches. Using the given slant height of 20 inches and π as 3.14, the lateral surface area can be calculated as follows:

A = πrl = 3.14 × 7 inches × 20 inches =
`3.14 X 140 inches^2`

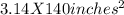
Therefore, after rounding to the nearest hundredth, the surface area of the cone peak is 439.60 square inches.

Answer 2

the surface area is approximately 439.60 square inches.

Step-by-step explanation:

To find the surface area of the cone peak, we need to find the lateral area by using the formula:

A = πr

where A is the lateral area, π is a constant with an approximate value of 3.14, r is the radius of the base of the cone, and s is the slant height of the cone

Given that the diameter of the base is 14 inches, the radius is half of that, so r = 7 inches. And the slant height is given as 20 inches.

Plugging these values into the formula, we get:

A = 3.14 × 7 × 20

= 439.6 square inches

Rounding to the nearest hundredth, the surface area of the cone peak is approximately 439.60 square inches.