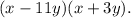The factored form of the expression
 is
is
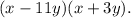
To factor the expression
 , we need to find two binomials whose product is equal to the given expression.
, we need to find two binomials whose product is equal to the given expression.
The general form of the quadratic expression
 can be factored into
can be factored into
 , where p, q, r, and s are constants. In this case, we have:
, where p, q, r, and s are constants. In this case, we have:
![\[x^2 - 3xy - 33y^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7cnga8kkmij8hpi3upjkdj7wgi73hu64gt.png)
To factor this expression, we need to find two values m and n such that:
![\[mn = ac = (1)(-33) = -33\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pqnm1n4cczuxzx0w5oajnvu5w01aefsuws.png)
m + n = b = -3
The values m and n that satisfy these conditions are m = 11 and n = -3. Now, we can factor the expression:
![\[x^2 - 3xy - 33y^2 = (x - 11y)(x + 3y)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jysy6v7aznkomltygrndcv5jukru1obmna.png)
So, the factored form of the expression
 is
is