Question

A bucket always contains two balls. Ball colors are red and blue. Each stage in a process consists of two steps: selection and replacement. At each stage a ball is randomly selected and then replaced by a new ball, which with probability 0.8 is the same color, and with probability 0.2 is the opposite color, as the ball it replaces. If initially both balls are red, find the probability that the fifth ball selected is red. (You will find it helpful to first model this system as a Markov chain.)

Answer 1

Probability that the fifth ball selected is red = 0.705

Explanation:

Let

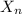`X_(n)` = Number of red balls after the 4th turn

⇒
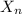`X_(n)` ∈ { 0, 1, 2 }

Then,

P =
`\left[\begin{array}{ccc}0.8&0.2&0\\0.1&0.8&0.1\\0&0.2&0.8\end{array}\right]`

⇒
`P^(4) = \left[\begin{array}{ccc}0.487&0.435&0.776\\0.218&0.565&0.218\\0.776&0.435&0.487\end{array}\right]`

Now,

P(5th ball is red |
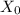`X_(0)` = 2 ) = 0.
`P^(4) _(20)` +
`(1)/(2)P^(4) _(21) + 1. P^(4) _(22)`

=
`(1)/(2) (0.4352) + 1. (0.4872) = 0.2176 + 0.4872`

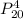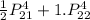
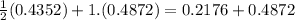
= 0.705

∴ we get

Probability that the fifth ball selected is red = 0.705