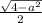Answer:
cosθ = ( √4 - a² ) ÷ 2
Step-by-step explanation:
sinθ = a/2
according to sincostan rule:
sinθ = opposite/ hypotenuse
cosθ = adjacent/ hypotenuse
so here opposite is a and hypotenuse is 2
adjacent² + opposite² = hypotenuse²
adjacent² + a² = 2²
adjacent = √4 - a²
we found our adjacent.
so cosθ = adjacent/ hypotenuse
= ( √4 - a² ) / 2
so cosθ =