Question

Milk with a density of 1020 kg/m3 is transported on a level road in a 9-m-long, 3-m-diameter cylindrical tanker. The tanker is completely filled with milk (no air space), and it accelerates at 4 m/s . If the minimum pressure in the tanker is 100 kPa, determine the maximum pressure difference and the location of the maximum pressure. Answer: 66.7 kPa

Answer 1

Given data is :

Density of the milk in the tank,
`$\rho = 1020 \ kg/m^3$`

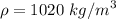
Length of the tank, x = 9 m

Height of the tank, z = 3 m

Acceleration of the tank,
`$a_x = 2.5 \ m/s^2$`

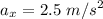
Therefore, the pressure difference between the two points is given by :

`$P_2-P_1 = -\rho a_x x - \rho(g+a)z$`

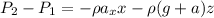
Since the tank is completely filled with milk, the vertical acceleration is
`$a_z = 0$`

`$P_2-P_1 = -\rho a_x x- \rho g z$`

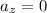
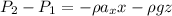
Therefore substituting, we get

`$P_2-P_1=-(1020 * 2.5 * 7) - (1020 * 9.81 * 3)$`

`$=-17850 - 30018.6$`

`$=-47868.6 \ Pa$`

`$=-47.868 \ kPa$`

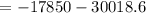
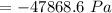
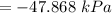
Therefore the maximum pressure difference in the tank is Δp = 47.87 kPa and is located at the bottom of the tank.