Question

The radius of a sphere is increasing at a constant rate of 8 meters per second. At the instant when the radius of the sphere is 22 meters, what is the rate of change of the volume? The volume of a sphere can be found with the equation V, equals, start fraction, 4, divided by, 3, end fraction, pi, r, cubed, .V=

3
4
​
πr
3
. Round your answer to three decimal places.

Answer 1

To find the rate of change of the volume of the sphere, differentiate the volume formula with respect to time using the chain rule. The rate of change of the volume is given by dV/dt = (4/3)π(22)² * 8, which simplifies to dV/dt = 38720π meters cubed per second.

To find the rate of change of the volume, we need to differentiate the volume formula with respect to time.

Given that the volume of a sphere is V = (4/3)πr³, where r is the radius of the sphere, we need to differentiate this volume formula with respect to time.

Using the chain rule, we have dV/dt = dV/dr * dr/dt.

The rate of change of the volume of the sphere is given by dV/dt, and the rate of change of the radius is dr/dt.

Since the radius is increasing at a constant rate of 8 meters per second, dr/dt = 8.

Substituting the given values into the equation, we have

`dV/dt = (4/3)\pi(22)^2 * 8.`

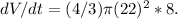
Simplifying, we get dV/dt = 38720π meters cubed per second.