Answer:
She scored in the 90th percentile.
90th percentile is better than 90% of the students who took the test, so yes, she will be admitted.
Explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
The scores on this test are known to be normally distributed with a mean of 725 and a standard deviation of 115.
This means that
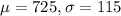
She must score better than at least 75% of the students who took the test.
So her z-score should have a pvalue of at least 0.75.
Harriet takes the test and scores 874.5. 1. (2pts) What percentile did Harriet score in?
We have to find the pvalue of Z when X = 874.5.

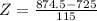
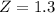
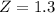 has a pvalue of 0.9032
has a pvalue of 0.9032
She scored in the 90th percentile.
Will Harriet be admitted?
90th percentile is better than 90% of the students who took the test, so yes, she will be admitted.