14. The solutions for
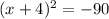 are complex:
are complex:
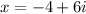 and
and
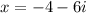 .
.
16. The solutions for
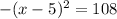 are complex:
are complex:

18. The solutions for
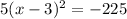 are complex:
are complex:
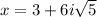 and
and
 .
.
20. The solutions for
 are complex:
are complex:
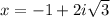 and
and
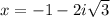 .
.
Let's solve each equation step by step using the square roots method:
### 14.
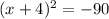
1. Expand the equation:
\((x+4)^2 = x^2 + 8x + 16\)
2. Set the equation equal to -90:
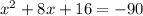
3. Move all terms to one side to form a quadratic equation:
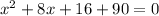
4. Combine like terms:
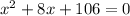
5. Use the quadratic formula to find solutions:
![\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]](https://img.qammunity.org/2024/formulas/mathematics/college/n2775bpyhr6nkttp819uth89i6m8ha2p28.png)
For this equation,
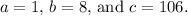
![\[ x = (-8 \pm √(8^2 - 4(1)(106)))/(2(1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lsoy2qznb5rfpa9t9fogdzq3tmmkedfp8n.png)
![\[ x = (-8 \pm √(64 - 424))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b6p0345z1fqr1ie1lpymzfzco7yo32htul.png)
![\[ x = (-8 \pm √(-360))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/34mzjcsplcdlbjqqh1ccy9p8sf0les59f5.png)
The discriminant
 is negative, so the solutions are complex. The solutions are:
is negative, so the solutions are complex. The solutions are:
![\[ x = -4 + 6i \quad \text{and} \quad x = -4 - 6i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tqzy03nv789cnwk3xj02r10iouw7gwqwty.png)
### 16.
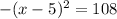
1. Remove the negative sign by multiplying both sides by -1:
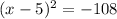
2. Expand the equation:
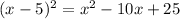
3. Set the equation equal to -108:

4. Move all terms to one side:
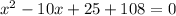
5. Combine like terms:
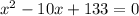
6. Use the quadratic formula:
For this equation,
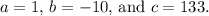
![\[ x = (10 \pm √((-10)^2 - 4(1)(133)))/(2(1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yq7jxsl6ck4xlywvy2wu0bbita0l2nn4ny.png)
![\[ x = (10 \pm √(100 - 532))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/189m2vl8bh5yq6bjt82jaevg8k82jrqzc0.png)
![\[ x = (10 \pm √(-432))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1qquzvsg2vyqgsbd8w5dw8g46lidd36ojx.png)
The discriminant is negative, so the solutions are complex. The solutions are:
![\[ x = 5 + 6√(3)i \quad \text{and} \quad x = 5 - 6√(3)i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/41jebjdp5h6lr0j4fmcnxk828uj2oqk0ld.png)
### 18.
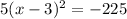
1. Divide both sides by 5 to simplify:
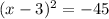
2. Expand the equation:
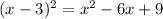
3. Set the equation equal to -45:
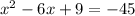
4. Move all terms to one side:

5. Combine like terms:
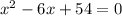
6. Use the quadratic formula:
For this equation,
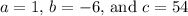 .
.
![\[ x = (6 \pm √((-6)^2 - 4(1)(54)))/(2(1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/g9s28imxzl9rxj71y9z4twf7819wd40hxr.png)
![\[ x = (6 \pm √(36 - 216))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mojtu7ol8kvlsa1c3kjprmngi9ufnvh2th.png)
![\[ x = (6 \pm √(-180))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9jgfigh1z0gy0y4hcd6xqxru8strv552n8.png)
The discriminant is negative, so the solutions are complex. The solutions are:
![\[ x = 3 + 6i√(5) \quad \text{and} \quad x = 3 - 6i√(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/d2tfusiez0bzq85jcj9bg22y7927ows6l5.png)
### 20.

1. Divide both sides by
 to simplify:
to simplify:

2. Expand the equation:

3. Set the equation equal to -12:
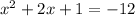
4. Move all terms to one side:
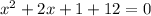
5. Combine like terms:
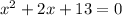
6. Use the quadratic formula:
For this equation,
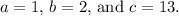
![\[ x = (-2 \pm √(2^2 - 4(1)(13)))/(2(1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pfo8lyuqfybkcz0hbdvauo9p1nwqzccu6u.png)
![\[ x = (-2 \pm √(4 - 52))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s1z9kxf8nzq74hmtdgail6v6nk6452qady.png)
![\[ x = (-2 \pm √(-48))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tyo6l0ilg1zazusib80zxgscjyc9eiipyu.png)
The discriminant is negative, so the solutions are complex. The solutions are:
![\[ x = -1 + 2i√(3) \quad \text{and} \quad x = -1 - 2i√(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/az18ndspoedah6kyi4yg3r4ejzowbedz64.png)
These are the solutions for the given equations, expressed in complex form.