Question

The length of a rectangular garden is 6 feet less than 5 times its width. Its area is 235 square feet.

Answer 1

Length = 31.4 ft

Width = 7.48 ft

Explanation:

Let's denote the width of the rectangular garden as
`\sf w` (in feet) and the length as
`\sf l` (in feet).

According to the given information:

The length is 6 feet less than 5 times the width:

`\sf l = 5w - 6`

The area of the rectangular garden is 235 square feet:

`\sf \text{Area} = l * w`

`\sf 235 = (5w - 6) * w`

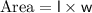
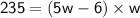
Now, let's set up and solve the equation to find the values of
`\sf w` and
`\sf l`:

`\sf 235 = (5w - 6) * w`

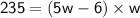
Expand the equation:

`\sf 235 = 5w^2 - 6w`

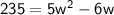
Set the equation equal to zero:

`\sf 5w^2 - 6w - 235 = 0`

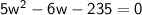
Now, we can either factor the quadratic equation or use the quadratic formula to solve for
`\sf w`.

Let's use the quadratic formula:

`\sf w = (-b \pm √(b^2 - 4ac))/(2a)`

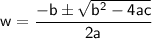
For the given equation
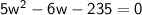`\sf 5w^2 - 6w - 235 = 0`, the coefficients are
`\sf a = 5`,
`\sf b = -6`, and
`\sf c = -235`.

`\sf w = (-(-6 ) \pm √((-6)^2 - 4(5)(-235)))/(2(5))`

Simplify the expression under the square root and calculate:

`\sf w = (6 \pm √(36 + 4700))/(10)`

`\sf w = (6 \pm √(4736))/(10)`

`\sf w = (6 \pm 68.818602136341 )/(10)`

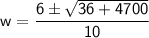
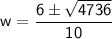
This gives two potential values for
`\sf w`. However, since the width cannot be negative, we discard the negative solution:

So,

`\sf w = (6 + 68.818602136341)/(10) \\\\ = (74.818602136341)/(10) \\\\ = 7.4818602136341 \\\\ = 7.48 \textsf{(in nearest hundredth)}`

Now that we have the width
`\sf w`, we can find the length
`\sf l` using the relationship
`\sf l = 5w - 6`:

`\sf l = 5(7.48) - 6 = 37.4 - 6 = 31.4`

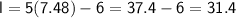
Therefore, the width of the rectangular garden is 7.48 feet, and the length is 31.4 feet.