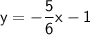Answer:
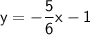
Explanation:
To find the equation of a line. let's take two points (-6,4) and (6,-6)
When two points are given:
 and
and
 , we can use the slope-intercept form:
, we can use the slope-intercept form:
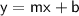
where
 is the slope and
is the slope and
 is the y-intercept. The slope
is the y-intercept. The slope
 is given by:
is given by:

Let's use the points
 and
and
 to find the slope:
to find the slope:
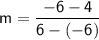

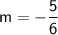
Now that we have the slope
 , let's use one of the points (let's use
, let's use one of the points (let's use
 ) to find the y-intercept
) to find the y-intercept
 :
:
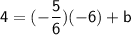
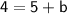
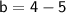

Now that we have the slope
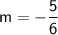 and the y-intercept
and the y-intercept
 , we can write the equation of the line in slope-intercept form:
, we can write the equation of the line in slope-intercept form:
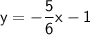
So, the equation of the line in fully simplified slope-intercept form is: