Question

Consider a particle in a 1-dimensional box defined by V(x)=0, for 0

Answer 1

The question is incomplete. The complete question is :

Consider a particle in a one-dimensional box defined by V(x)=0, a>x>0 and V(x)=infinity, x a, x 0. Explain why each of the following un-normalized functions is or is not an acceptable wave function based on criteria such as being consistent with the boundary conditions, and with the association of psi^+(x)psi(x)dx with the probability.

a).
`$A \cos (n \pi x)/(a)$`

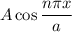
b).
`$B(x+x^2)$`

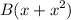
c).
`$Cx^3(x-a)$`

d).
`$(D)/(\sin (n \pi x)/(a))$`

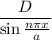
Solution :

a). The function of cosine here do not go to the value 0 at the boundary of the box (that is to be expected as V is infinite there).

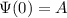`$ \Psi (0) = A$` and
`$ \Psi (a) = A \cos(n \pi) = \pm 1$`

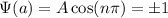
Therefore it is not an acceptable function.

b). The function in this case goes to 0 at
`$x=0, $` but is non zero at
`$x=a$`. So this function is also not acceptable.

c). The function here goes to 0 at both
`$x=a$` and
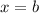`$x=b$` . But this wavelength can never satisfy the time independent Schrodinger equation.

`-(\hbar^2)/(2m)(d^2)/(dx^2)\Psi(x)\\eq E\Psi(x)\quad \text{for} \ \quad \Psi(x)=Cx^3(x-a)`

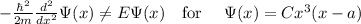
Therefore,
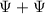`$\Psi + \Psi $` here can not be associated with the probability.

d). Here, the function goes to the infinite at
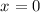`$x=0 $` and
`$x=a$`. Thus this is also not valid choice for the wave function.