Question

A lawn seed mixture contains three types of seed: bluegrass, rye, and Bermuda. The costs per pound of the three types of seed are 12 cents, 14 cents, and 3 cents, respectively. In each batch there must be at least 25% bluegrass seed, and the amount of Bermuda must be no more than 2/3 the amount of rye. To fill current orders, the company must make at least 6000 pounds of the mixture. How much of each kind of seed should be used to minimize cost

Answer 1

612 dollars

Explanation:

From the given information:

Amount of the total mixture = 6000 pounds

Also, for each batch, there needs to be at least 25% bluegrass seed.

It implies that:

In 6000 pounds, there are (25×6000)/100 = 1500 pounds of bluegrass seed.

The remaining amount of (6000 - 1500 = 4500)pounds will be for rye and Bermuda.

Suppose the amount of rye seeds = x pounds

while that of Bermuda is (4500 - x) pounds

Then, since the amount of Bermuda contains no more than 2/3 of that of rye.

The equation can be written as:

`( 4500 - x) = (2x)/(3)`

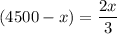
13500 - 3x = 2x

13500 = 5x

`x = (13500)/(5)`

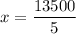
x = 2700

Now, the amount of rye seed = 2700 pounds

while that of Bermuda seed = 4500 - 2700 = 1800 pounds

However, For Bluegrass, we are told that the cost of 1 pound is 12 cents.

So, the cost of 1500 bluegrass seeds = 12 × 1500 = 18000 cents

For rye seed; cost of 1 pound = 14 cents

the cost of 2700 rye seeds = 14 × 2700 = 37800 cents

For Bermuda seed; cost of 1 pound = 3 cents

the cost of 1800 rye seeds = 3 × 1800 = 5400 cents

The total amount = (18000 + 37800 + 5400) = 61200 cents

Recall that:

100 cents = 1 dollars

61200 cents = x dollars

x = 61200 cents/100 cents

x = 612 dollars

Thus, the minimum cost is 612 dollars.