Answer:
a)
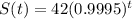
b) It will take 10,692 years.
Explanation:
Exponential function to determine the amount of substance:
An exponential function to determine the amout of substance after t years is given by:
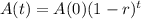
In which A(0) is the initial amount and r is the decay rate, as a decimal.
(a) Write an equation to determine the amount of substance, S, left after t years.
Half-life of 1300 years means that
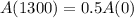 .
.
We use this to find r. So
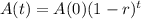
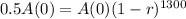
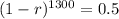
![\sqrt[1300]{(1-r)^(1300)} = \sqrt[1300]{0.5}](https://img.qammunity.org/2022/formulas/mathematics/college/zjevtam84xr9cf8j59v5wpa7qaxcklw1cz.png)
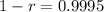
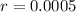
Sample of 42 grams means that
 . So
. So
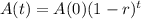
Replacing A by S, just for notation purposes
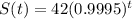
(b) Approximately how long will it take for 0.2 grams of substance to remain (to the nearest year)?
This is t when
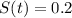 . So
. So
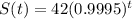
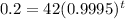
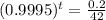
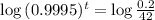
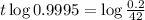
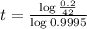
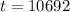
It will take 10,692 years.