Question

Triangle ABD~ triangle DBC the perimeter of triangle ABD=36, fond the perimeter of triangle DBC.

Answer 1

Perimeter of ΔDBC = 48 units

Explanation:

It's given in he question,

ΔABD ~ ΔDBC

Therefore, by the definition of similar triangles,

Corresponding sides of both the triangle will be proportional.

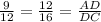
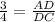
`(AB)/(DB)= (BD)/(BC)= (AD)/(DC)`

`(9)/(12)= (12)/(16)= (AD)/(DC)`

`(3)/(4)=(AD)/(DC)`

AD =
`(3)/(4)DC` ----------(1)

Since, perimeter of ΔABD = 36,

AB + BD + AD = 36

9 + 12 + AD = 36

AD = 36 - 21

AD = 15

From equation (1),

15 =
`(3)/(4)(DC)`

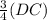
DC = 20

Perimeter of ΔDBC = DB + BC + DC

= 12 + 16 + 20

= 48

Therefore, perimeter of ΔDBC = 48 units is the answer.