Final Answer:
To model a snowboarder's motion during a jump, you can use the equations of motion for projectile motion. Considering the rider as a projectile, you can use the kinematic equations to describe their vertical and horizontal motion. For vertical motion, the equation
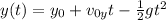 can be used, where
can be used, where
 is the initial height,
is the initial height,
 is the vertical component of the initial velocity, (t) is time, and (g) is the acceleration due to gravity. For horizontal motion, the equation
is the vertical component of the initial velocity, (t) is time, and (g) is the acceleration due to gravity. For horizontal motion, the equation
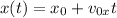 can be used, where
can be used, where
 is the initial horizontal position, and
is the initial horizontal position, and
 is the horizontal component of the initial velocity.
is the horizontal component of the initial velocity.
Step-by-step explanation:
In vertical motion, the equation
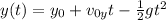 describes the snowboarder's height at any given time during the jump. Here,
describes the snowboarder's height at any given time during the jump. Here,
 is the initial height,
is the initial height,
 is the vertical component of the initial velocity, (t) is time, and (g) is the acceleration due to gravity
is the vertical component of the initial velocity, (t) is time, and (g) is the acceleration due to gravity
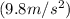 . This equation takes into account the initial height, the initial upward velocity, and the effect of gravity on the snowboarder's height.
. This equation takes into account the initial height, the initial upward velocity, and the effect of gravity on the snowboarder's height.
For horizontal motion, the equation
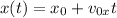 describes the snowboarder's horizontal position at any time during the jump. Here,
describes the snowboarder's horizontal position at any time during the jump. Here,
 is the initial horizontal position,
is the initial horizontal position,
 is the horizontal component of the initial velocity, and (t) is time. This equation assumes constant horizontal velocity, neglecting air resistance.
is the horizontal component of the initial velocity, and (t) is time. This equation assumes constant horizontal velocity, neglecting air resistance.
By solving and analyzing these equations, you can gain insights into the snowboarder's trajectory during a jump. Numerical methods like Euler or Runge-Kutta can be applied to simulate the motion, allowing you to investigate the feasibility of a quintuple cork under different initial conditions for the jump and rider.