Question

g Suppose that an escalator raises stationary passengers vertically at a speed of ten feet per second, and the escalator is pointing northeast so its passengers also move northeast at ten feet per second. If a child riding the escalator drops a ball so that it rolls north on the escalator at a speed of 5 feet per second, what is the speed of the ball relative to a stationary observer

Answer 1

v = 14 ft / s, 49.6º north of east

Step-by-step explanation:

This is a relative velocity problem, let's use subscripts to work

* e for the escalator

* p for ball

velocity is a vector whereby

v = v_e + v_p

The bold are vector. An easy way to work with this type of problem is to decompose the velocities into a Cartesian coordinate system, where the x-axis coincides with East and the y-axis with North.

stair speed

sin 45 = v_{ey} / ve

cos 45 = v_{ex} / ve

v_{ey} = go sin 45

v_{ex} = ve cos 45

v_{ey} = 10 sin 45 = 7.07 ft / s

v_{ex} = 10 cos 45 = 7.07 ft / s

the speed of the ball is

v_p = 5 j ^ ft / s

therefore the speed that the observer sees is

X axis

vₓ = v_{ex}

vₓ = 7.07 ft / s

Y axis

v_y = v_{ey} + v_p

v_y = 7.07 + 5

v_y = 12.07 ft / s

we can give the result in two ways

* v = (7.07 i ^ +12.07 j ^) ft / s

* in module and angle form

Let's use the Pythagorean theorem

v =
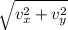
`√(v_x^2 + v_y^2)`

v =
`√(7.07^2 +12.07^2)`

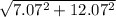
v = 13.99 ft / s

v = 14 ft / s

we use trigonometry

tan θ = vy / vx

θ = tan⁻¹ v_y / vₓ

θ = tan⁻¹ 12.07 / 7.07

θ = 49.6º

in the form of cardinal coordinates they are 49.6º north of east