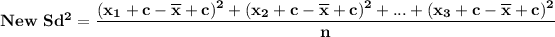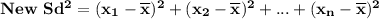Question

Suppose that a nonzero constant b is added to every value of a generic sample dataset 1 2 3 { , , , , }n x x x x , to produce a new dataset 1 2 3 { , , , , } n x b x b x b x b . Provide a formal mathematical (i.e., algebraic) proof for what happens to the mean, variance, and standard deviation. (Hint: Think of the dotplot for informal motivation.)

Answer 1

Explanation:

Suppose there is the addition of a constant "b" to each generic dataset, then, new mean = old mean + b. This will affect the variance and the standard deviation of the resulting dataset to remain the same:

From the information given:

`\mathbf{x_1,x_2,x_3...x_n \ have \ mean \ \overline x }`

Proof:

If c is added to each data set:

Then,

`\mathbf{x_1+c,x_2+c,x_3+c...x_n+c \ and \ the \ new \ mean \ \overline x = \overline x + c}`

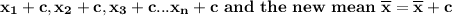
also;

`\mathbf{New \ Sd^2 = ((x_1+c -(\overline x+c))^2+ (x_2+c -(\overline x+c))^2 +...+ (x_3+c -(\overline x+c))^2)/(n)}`

`\mathbf{New \ Sd^2 = ((x_1+c -\overline x+c)^2+ (x_2+c -\overline x+c)^2 +...+ (x_3+c -\overline x+c)^2)/(n)}`

`\mathbf{New \ Sd^2 = (x_1- \overline x)^2+ (x_2- \overline x)^2+ ... +(x_n- \overline x)^2}`

`\mathbf{New \ Sd^2 = old \ sd^2}`